Overview
D-Claw is an open-source software package for modeling granular-fluid flows (landslides, debris flows, etc.) within the larger Clawpack open-source project. D-Claw implements a two-phase granular mathematical model developed by Richard Iverson and David George at the U.S. Geological Survey. See software for more information and links to source-code repositories, and projects for examples of D-Claw applications.
Granular-fluid mathematical model
The two-phase granular-fluid model implemented in D-Claw is based on mathematical models originally developed by Richard Iverson and later co-developed with David George, at the USGS. The model, described in detail by Iverson & George, 2014 and George & Iverson, 2014, combines principles of fluid, solid, and soil mechanics. A unique feature of the model is the coupled evolution of the solid-grain concentration and the basal pore-fluid pressure, based on the principles of granular dilatancy. This co-evolution mediates the coulomb effective stress and hence the mobility of the flow, and hence allows the simulation of slope failure, incipient motion, and deposition without unrealistic force balances. The governing PDEs form a strictly hyperbolic system with non-conservative products, sharing fundamental mathematical stability properties with the more basic shallow water equations. The development of this model was informed by controlled experiments conducted at the USGS debris-flow flume over the last ~ 30 years (flume video archives). The aim of those experiments was to investigate the complex physics of debris flow motion, including initiation processes. Experimental work at the flume is ongoing. For more details see publications below.
Ongoing research and model development
Ongoing D-Claw development is aimed at extending its capabilities to more general surface flow processes by accommodating diverse granular fluid mixtures and interactions between different flow types. Recent examples include landslide-generated tsunamis, seiches leading to erosive dam breaches, and erosive overland flows that transform into debris flows. Extension of D-Claw to post-wildfire debris flows based on these capabilities is an active area of collaboration. Previous D-Claw extensions related to particle-size segregation and levee formation (an important process for debris-flow dynamics) provides an additional topic of continued research. Rainfall infiltration and pore-pressure diffusion modeling are also actively under development.
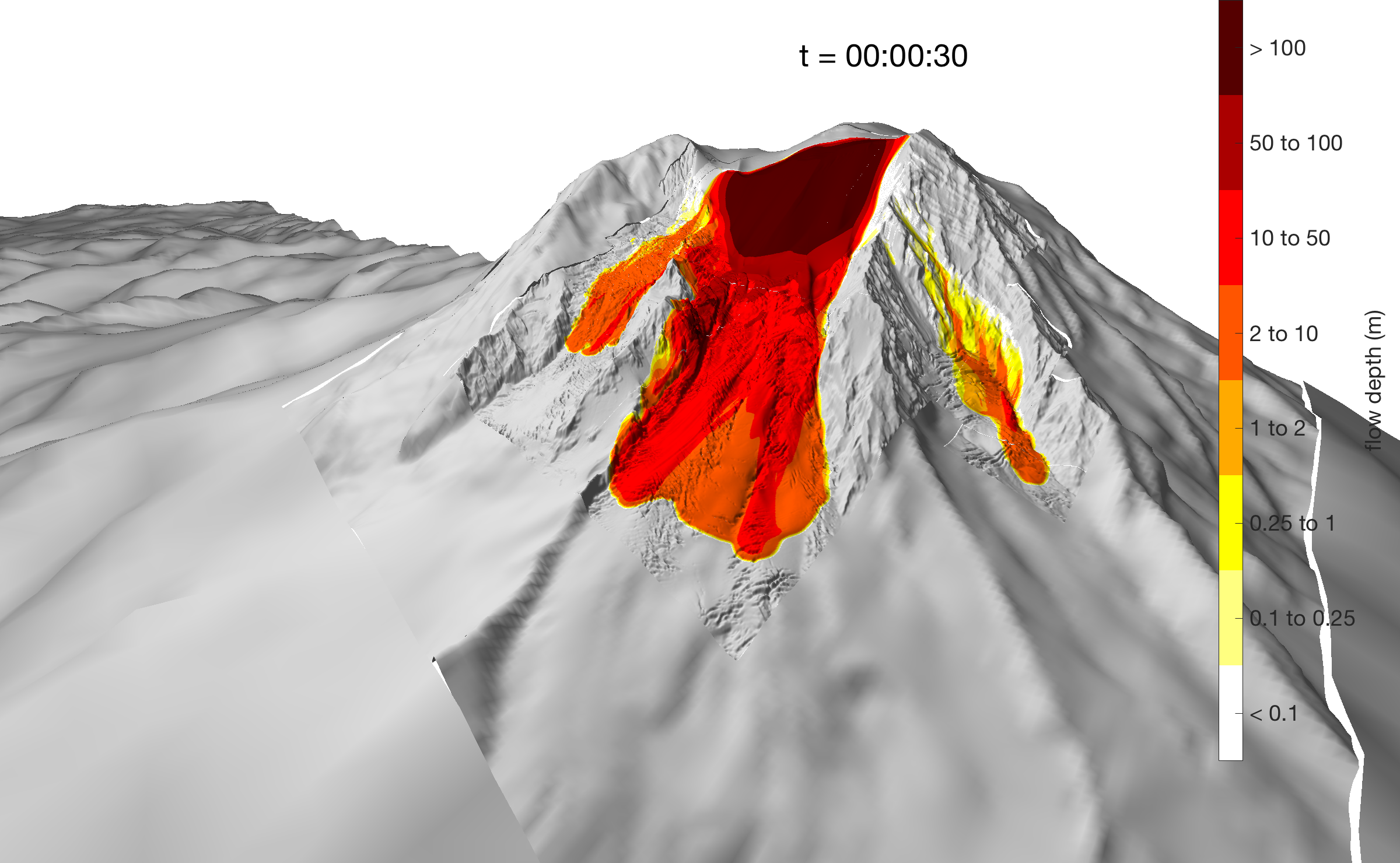
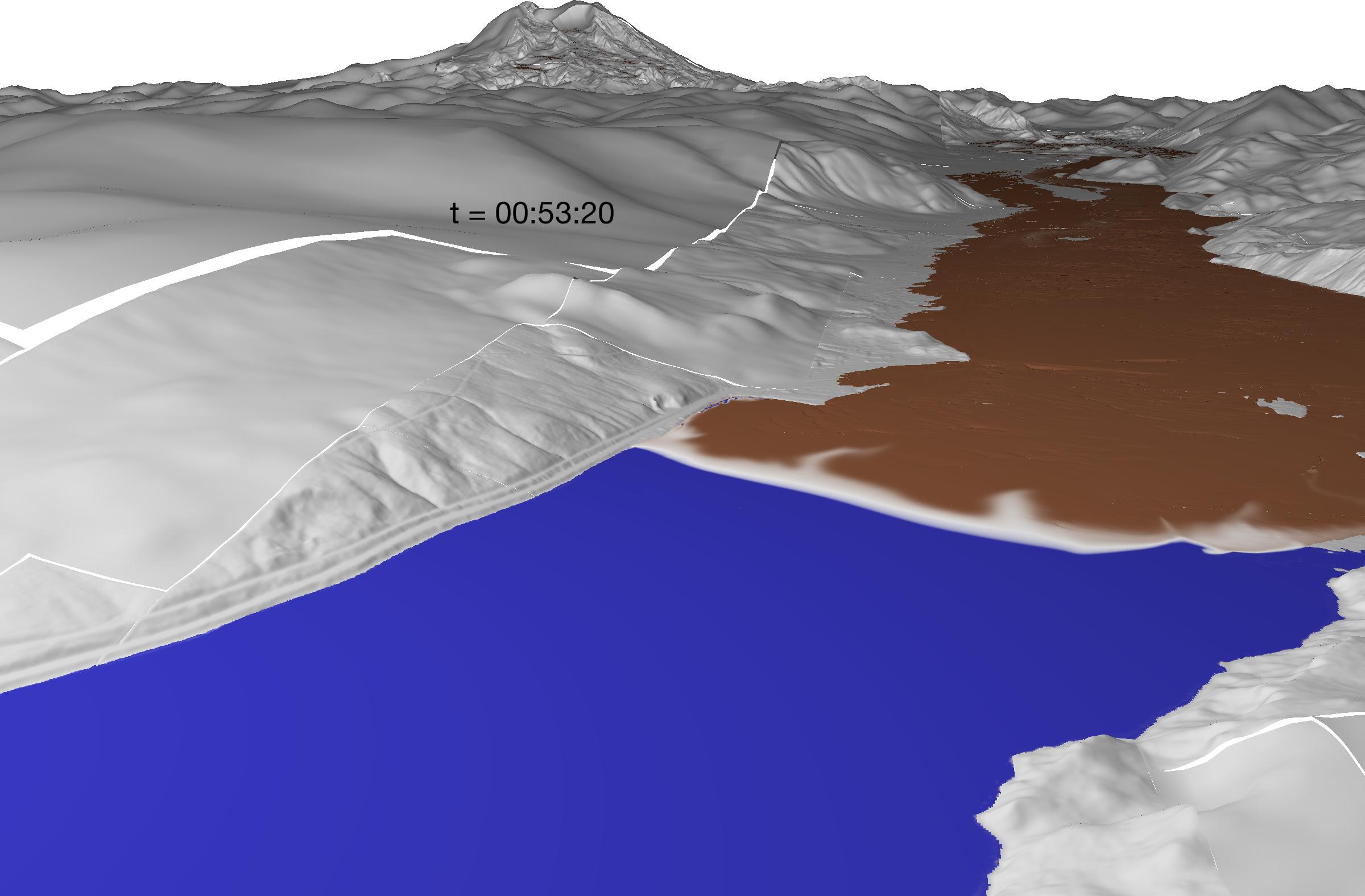
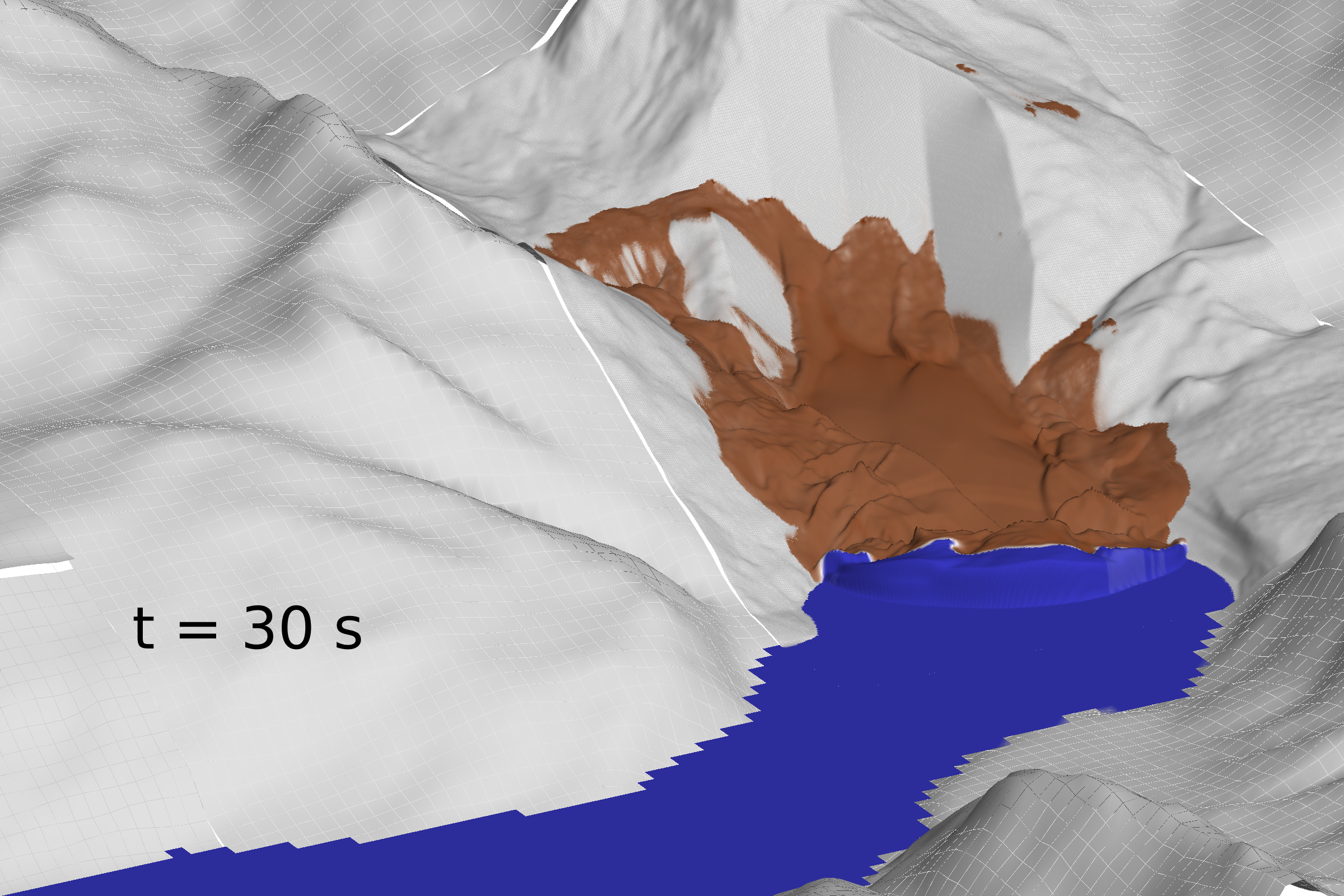
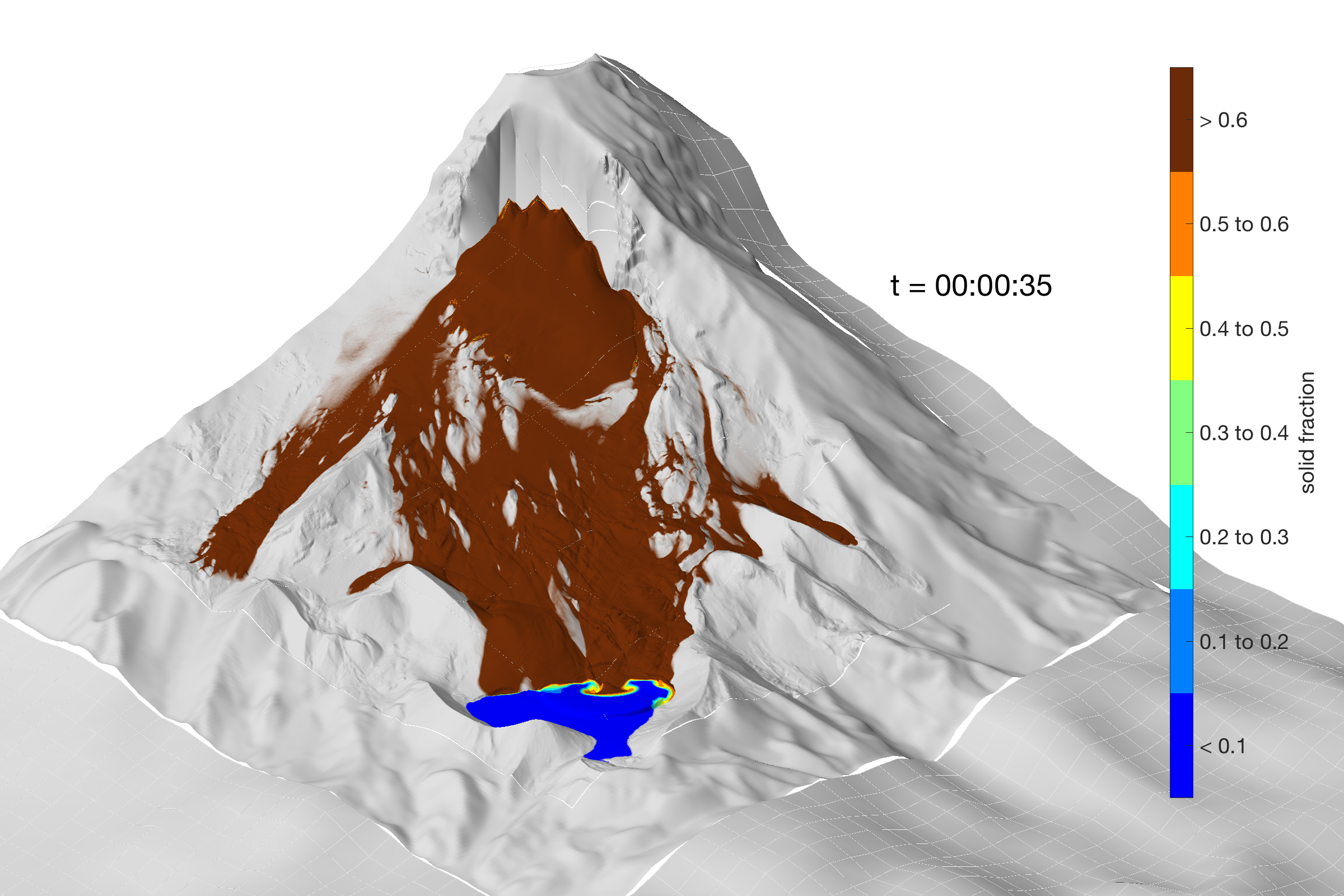
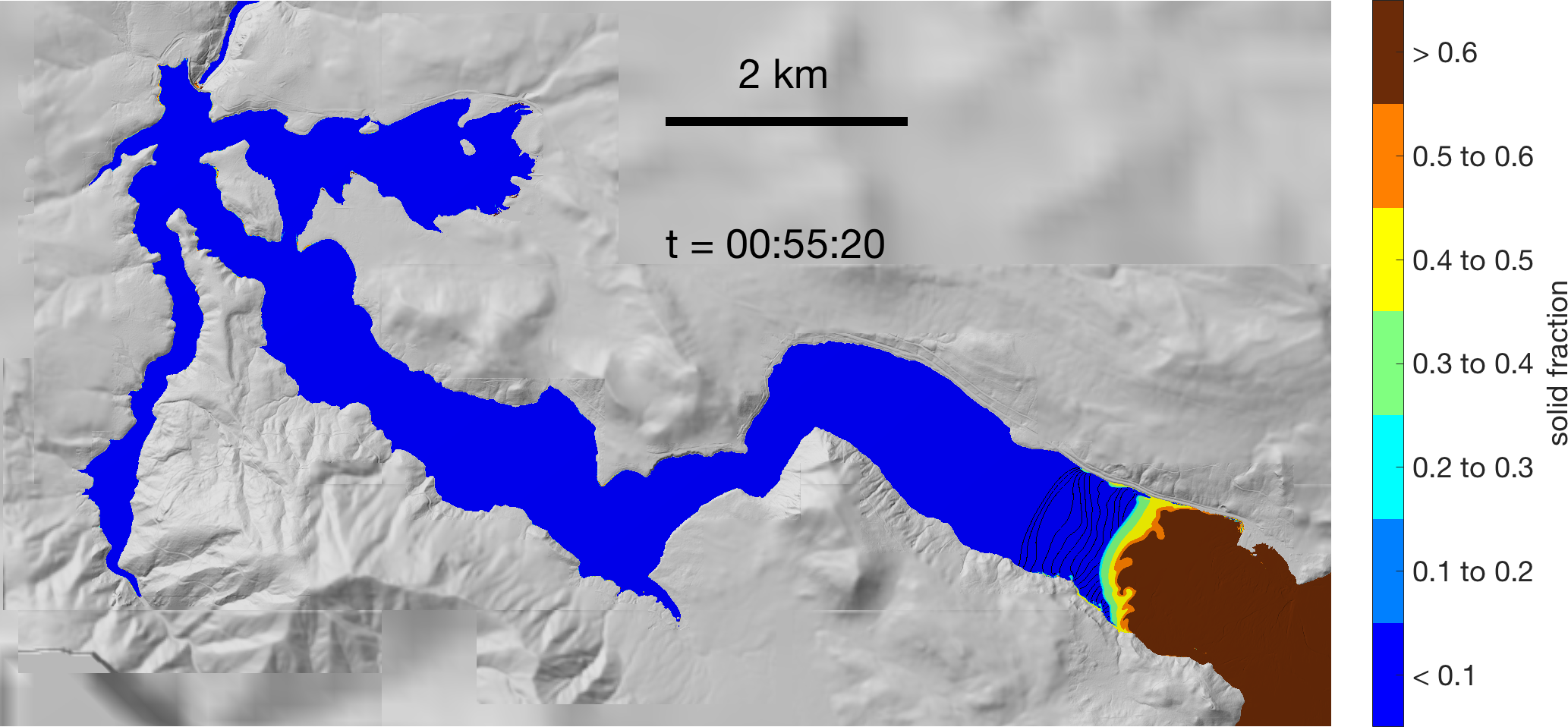
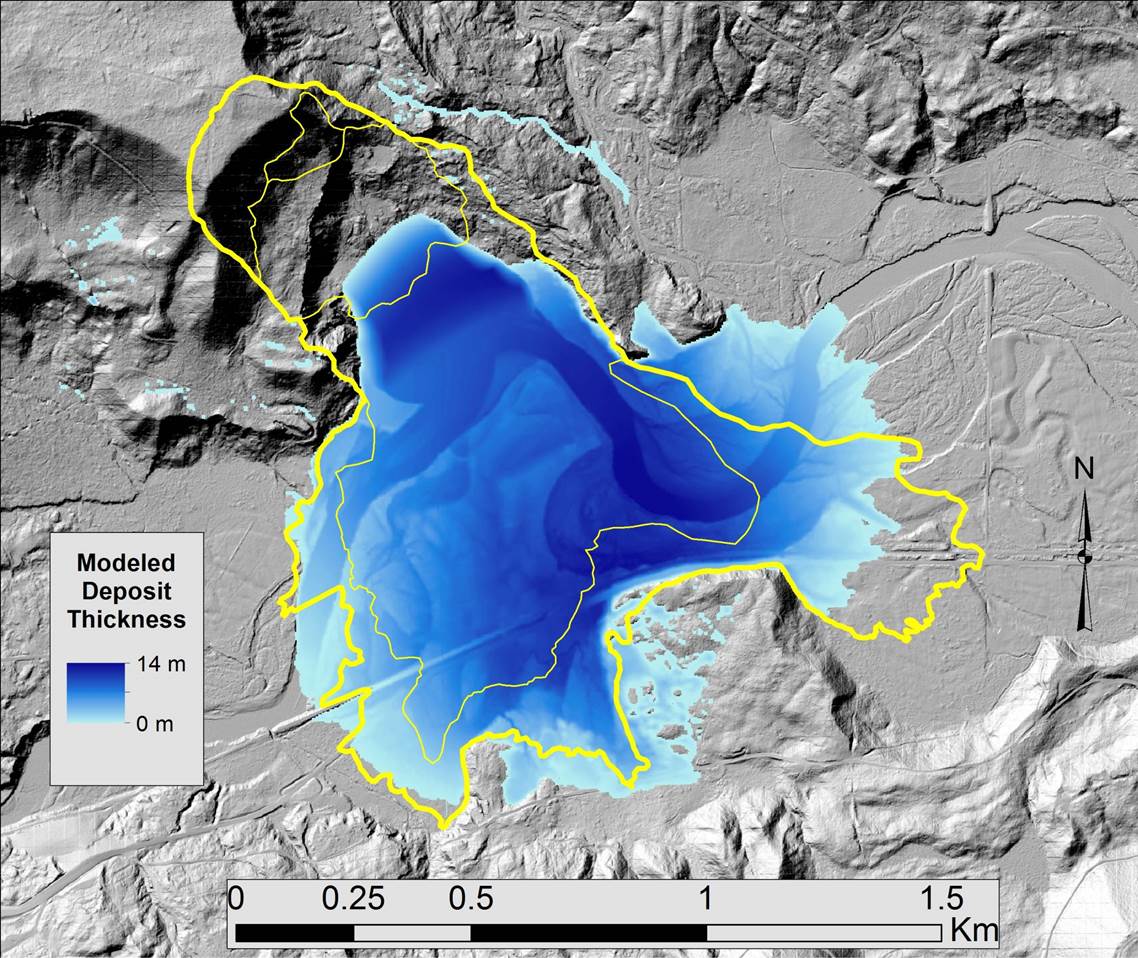
D-Claw slideshow
See individual projects for animations and background information related to D-Claw modeling studies.

References
- A depth-averaged debris-flow model that includes the effects of evolving dilatancy: 1. Physical basis. R. M. Iverson and D. L. George, 2014. Proc. R. Soc. A, 470 (2170). pdf
- A depth-averaged debris-flow model that includes the effects of evolving dilatancy: 2. Numerical predictions and experimental tests. D. L. George and R. M. Iverson, 2014. Proc. R. Soc. A, 470 (2170). pdf
- Landslides that liquefy: modeling mobility bifurcation and the 2014 Oso, Washington, USA disaster. R. M. Iverson, D. L. George, 2016. Geotechnique, V. 66(3), 175–187. pdf
- Landslide mobility and hazards: implications of the 2014 Oso disaster. R. M. Iverson, D. L. George, et al., 2015. Earth Planet. Sci. Lett., V. 412, pp. 197–208. pdf
- New methodology for computing tsunami generation by subaerial landslides: application to the 2015 Tyndall Glacier Landslide, Alaska. D. L. George, R. M. Iverson, C. M. Cannon, 2017. Geophys. Res. Lett., V. 44(14), 7276–7284. pdf
- Tsunami modeling with adaptively refined finite volume methods. R.J. LeVeque, D.L. George and M.J. Berger, 2011. Acta Numerica 20, pp. 211–289. Arieh Iserles, ed. pdf
- The GeoClaw software for depth-averaged flows with adaptive refinement. M. J. Berger, D. L. George, R. J. LeVeque and K. T. Mandli, 2011. Advances in Water Resources, 34: 1195–1206. doi: 10.1016/j.advwatres.2011.02.016. pdf
- Finite volume methods for hyperbolic problems. R.J. LeVeque, 2002. Texts in Applied Mathematics, Cambridge University Press.
- Local adaptive mesh refinement for shock hydrodynamics. M.J. Berger and P. Colella, 1989. J. Comput. Phys., 82: 64-84.
- Augmented Riemann solvers for the shallow water equations over variable topography with steady states and inundation. D. L. George, 2008. J. Comput. Phys., 227(6): 3089–3113. pdf
- Finite volume methods and adaptive refinement for tsunami propagation and inundation, D.L. George, 2006. Ph.D. thesis, University of Washington, Seattle. pdf